Câu 84 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1
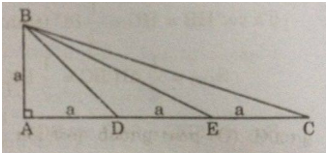
Tam giác ABC vuông tại A, AB = a, AC = 3a. trên cạnh AC lấy các điểm D, E sao cho
AD = DE = EC.
a) Chứng minh: ({{DE} over {DB}} = {{DB} over {DC}})
b) Chứng minh ∆BDE đồng dạng ∆CDB
c) Tính tổng (widehat {AEB} + widehat {BCD}) bằng hai cách
Cách 1: sử dụng kết quả ở câu b);
Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.
Gợi ý làm bài
a) Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
(B{D^2} = A{D^2} + A{B^2} = {a^2} + {a^2} = 2{a^2})
Suy ra: (BD = asqrt 2 )
Ta có:
(eqalign{& {{DE} over {DB}} = {a over {asqrt 2 }} = {{sqrt 2 } over 2}; cr & {{DB} over {DC}} = {{asqrt 2 } over {2a}} = {{sqrt 2 } over 2} cr} )
Vậy ({{DE} over {DB}} = {{DB} over {DC}})
b) Xét ∆BDE và ∆CDB, ta có:
({{DE} over {DB}} = {{DB} over {DC}},(1))
(widehat {BDE} = widehat {BDC},(2))
Từ (1) và (2) suy ra ∆BDE đồng dạng ∆CDB.
c) * Cách 1:
Ta có: ∆BDE đồng dạng ∆CDE (Rightarrow widehat {BED} = widehat {CBD})
Mặt khác:
(widehat {AEB} + widehat {BCD} = widehat {BED} + widehat {BCD} = widehat {CBD} + widehat {BCD},(3))
Trong ∆BCD, ta có:
(widehat {ADB} = widehat {CBD} = widehat {BCD}) (tính chất góc ngoài) (4)
(widehat {ADB} = 45^circ ) (vì ∆ABD vuông cân tại A) (5)
Từ (3), (4) và (5) suy ra: (widehat {AEB} + widehat {BCD} = 45^circ )
* Cách 2:
Trong tam giác ABC, ta có:
(tgwidehat {AEB} = {{AB} over {AC}} = {a over {2a}} = {1 over 2})
Suy ra: (widehat {AEB} = 26^circ 34′)
Trong tam giác vuông ABC, ta có:
(tgwidehat {ACB} = {{AB} over {AC}} = {a over {3a}} = {1 over 3})
Suy ra: (widehat {ACB} = 18^circ 26′)
Vậy: (widehat {AEB} + widehat {ACB} = widehat {AEB} + widehat {BCD} = 45^circ )
Câu 85 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1
(h.31) Tính góc α tạo bởi hai mái nhà, biết rằng mỗi mái nhà dài 2,34m và cao 0,8m.
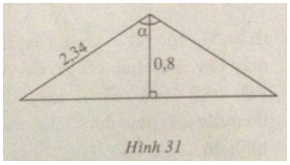
Gợi ý làm bài
Hai mái nhà bằng nhau tạo thành hai cạnh của một tam giác cân. Chiều cao cảu mái nhà chia góc ở đỉnh ra thành hai phần bằng nhau.
Ta có:
(cos {alpha over 2} = {{AH} over {AB}} = {{0,8} over {2,34}} approx 0,4319)
Suy ra: ({alpha over 2} = 70^circ )
Vậy (alpha = 140^circ ).
Câu 86 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hình 32.
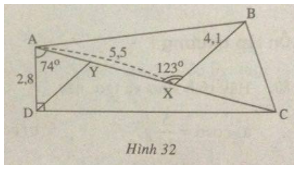
Biết:
(AD bot DC,widehat {DAC} = 74^circ )
(widehat {AXB} = 123^circ ,AD = 2,8,cm)
AX = 5,5cm, BX = 4,1cm.
a) Tính AC.
b) Gọi Y là điểm trên AX sao cho DY ⁄⁄ BX. Hãy tính XY
c) Tính diện tích tam giác BCX
Gợi ý làm bài
a) Trong tam giác vuông ACD, ta có:
(AC = {{AD} over {cos widehat {CAD}}} = {{2,8} over {cos 74^circ }} approx 10,158,(cm))
b) Kẻ (DN bot AC)
Trong tam giác vuông AND, ta có:
(eqalign{& DN = AD.sin widehat {DAN} cr & = 2,8.sin 74^circ approx 2,692,(cm) cr} )
(eqalign{& AN = AD.cos widehat {DAN} cr & = 2,8.cos 74^circ approx 0,772,(cm) cr} )
Vì BX // DY nên (widehat {D{rm{YX}}} = widehat {BXY} = 123^circ ) ( hai góc so le trong)
Mà (widehat {DYN} + widehat {D{rm{YX}}} = 180^circ ) (kề bù)
Suy ra:
(widehat {DYN} = 180^circ – widehat {D{rm{YX}}} = 180^circ – 123^circ = 57^circ )
Trong tam giác vuông DYN, ta có:
(eqalign{& NY = DN.cot gwidehat {DYN} cr & approx 2,692.cot g57^circ approx 1,748,(cm) cr} )
Ta có:
(eqalign{& XY = AX – (AN + NY) cr & = 5,5 – (0,772 + 1,748) = 2,98,(cm) cr} )
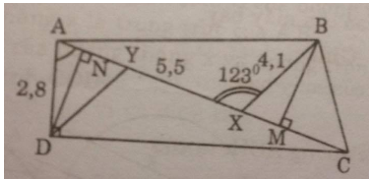
c) Ta có:
(CX = AC – AX approx 10,158 – 5,5 = 4,658,(cm))
Kẻ (BM bot CX)
Ta có:
(widehat {BXC} = 180^circ – widehat {BXA} = 180^circ – 123^circ = 57^circ )
Trong tam giác vuông BMX, ta có:
(eqalign{& BM = BX.sin widehat {BXC} cr & = 4,1.sin 57^circ approx 3,439,(cm) cr} )
(eqalign{& {S_{BCX}} = {1 over 2}BM.CX cr & = {1 over 2}.3,439.4,658 = 8,009,left( {c{m^2}} right). cr} )
Câu 87 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1
Tam giác ABC có (hat A = 20^circ ,widehat B = 30^circ ,AB = 60cm). Đường vuông góc kẻ từ C đến AB cắt AB tại P. (h.33).
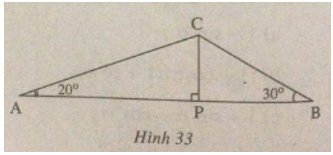
Hãy tìm:
a) AP, BP;
b) CP.
Gợi ý làm bài
a) Trong tam giác vuông ACP, ta có:
(AP = CP.cot gwidehat {PAC},(1))
Trong tam giác vuông BCP, ta có:
(BP = CP.cot gwidehat {PBC},(2))
Từ (1) và (2) suy ra:
((AP + BP) = CP.cot gwidehat {PAC} + CP.cot gwidehat {PBC})
Hay (AB = CP(cot gwidehat {PAC} + cot gwidehat {PBC}))
Suy ra:
(eqalign{& CP = {{AB} over {cot gwidehat {PAC} + cot gwidehat {PBC}}} cr & = {{AB} over {cot g20^circ + cot g30^circ }} approx 13,394,(cm) cr} )
b) Thay CP = 13,394 vào (1) ta có:
(AP = 13,394.cot g20^circ approx 36,801,(cm))
Thay CP = 13,394 vào (2) ta có:
(BP = 13,394.cot g30^circ approx 27,526,(cm))
Giaibaitap.me
